- An Introduction to Graph Algorithms
Post Stastics
- This post has 1327 words.
- Estimated read time is 6.32 minute(s).
This post marks the first in a series of posts I will complete on graph algorithms. The code will be python however, I will write the code very verbosely so it will be easily ported to your favorite programming language. I will assume you have some programming skills but are still a novice or that you have been programming for some time now but have not learned anything about graphs, how to implement them or how to use them. So let’s get started!
A graph in computer science is a non-linear data structure that consists of nodes (vertices) and edges (lines connecting the nodes together).
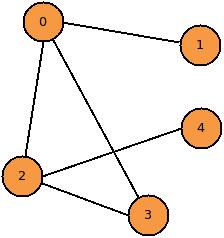
Referring to figure 1 above, nodes 0,1,2,3, and 4 form a graph. This graph is an acyclic graph, meaning it has no cycles (loops). A-cyclic graphs are also known as trees, and standard breadth-first and depth-first algorithms work well with them. A graph is said to have cycles when a combination of edges in the graph form a closed path. In other words, a loop.
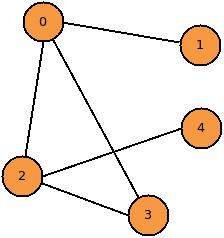
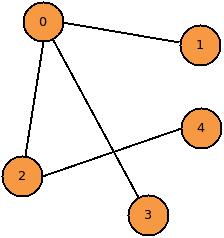
Looking at figure 2, you can see the loop formed by the path 0->2->3->0 and 0->3->2->0. In this non-directed graph, these two paths are equivalent. More complex graphs may have directed edges. If the graph in figure 2 had directional arrows on the edges, it would be a directed graph and the paths 0->2->3->0 and 0->3->2->0 would be different paths. You can think of non-directed graphs having two-way streets for edges and directed graphs as having one-way streets for edges.
Graphs have many uses in computer science. They can be used to model social interaction and network traffic or even the flow of water or traffic in a city. Graphs are important for pathfinding as well. They are applicable to many computer-science problems and therefore it is very handy to know about graphs and how to use them in your code.
Representing Graphs
The first thing one must ask when learning a new data structure is “How do I represent it to the computer?”. In the case of graphs, this question can have many answers, and which answer is right for you depends entirely on what you need to accomplish, and what resources are available.
One of the simplest ways to represent a graph is using an adjacency list. There are other ways such as adjacency matrix, incidence list, and tree type structures.
Adjacency List
Implementing an adjacency list is simple. We use a list (array) to represent the node. So index 0 of the array represents node 0 of the graph, index 1 of the array represents node 1, and so forth. In each index, in the array, we place a list of connected nodes. This represents the connecting edges. So if node 0 is connected by an edge to node four, index 0 of the array will contain a list containing the value 4.
// figure 1 graph in python graph = [[1,2,3], [0], [0,4], [0], [2]]
The above Python code represents the graph in figure 1. As you can see the list stored at index 0 contains all the nodes that connect to node 0. Node 2 connects to both node 0 and node 4, etc. This arrangement can also be implemented using linked lists or vectors in other languages.
It should be noted here that the code above represents a non-directed graph. So each node must hold a reciprocal path. For example, node 2 connects to node 4. So, node 4 must also connect to know 2. This isn’t true of directed graphs. You might wonder why you might use a directed graph. They can be used to model things like which way water is flowing in a pipe, or the direction of traffic on a road, or current in a circuit, and much more.
Walking the Graph
Graphs are not much help unless you can walk them. While our demo will only print the nodes we visit, you’ll usually want to do some work on or with each node. But before we get into that, let’s focus on how to visit each node.
Depth-First Ordering
When it comes to visiting nodes there are two primary orders in which we can walk the graph. A Breath first-order means we visit a node and its siblings before visiting the node’s children. A depth-first order means we visit a node’s children first and then the node’s siblings. For example, using figure 1 as our graph, in breadth-first order we would visit node 0 then any of nodes 2,3,1 then node 4. In depth-first order, we would visit node 0 than any of 1,2,3. However, when we visited node 2 we would immediately visit node 4 before going to the next sibling of node 2.
One of the simplest ways to manage the nodes is to use a stack or queue. You would use a stack for depth-first order and a queue for breath-first order. I suggest you walk through the algorithm using the stack and then a queue to fully understand why changing the data structure changes the order.
Let’s see some code for walking the graph:
#
# Simple Graph Example
#
def visit_depth_first(graph, start_node):
stack = []
visited = []
stack.append(start_node)
# While stack not empty
while stack:
# Get next node
current_node = stack.pop()
# if already visited, skip
if current_node in visited:
continue
# mark as visited
visited.append(current_node)
# Get current node's children
children = graph[current_node]
# Add current_node's children to stack
for child in children:
stack.append(child)
# Display the current node
print(f'Visiting node {current_node}')
if __name__ == '__main__':
graph = [[1,2,3], [0], [0,4], [0], [2]]
visit_depth_first(graph, 0)
Read the code and comments. I truly over-commented this code for the newbies out there. Read this code and try to understand it. It really isn’t very complex. Experiment with the code. Comment out the lines that add a node to the visited list and see how that affects the run. Once you think you understand the code and how it works, try writing it from scratch without peeking.
# Output from running visit_depth_first Visiting node 0 Visiting node 3 Visiting node 2 Visiting node 4 Visiting node 1
Breadth-First Ordering
Now, let’s see how we would visit the nodes in a breath first (siblings first) order:
...
def visit_breath_first(graph, start_node):
visited = []
queue = []
queue.append(start_node)
while queue:
# Get next node
current_node = queue.pop(0)
if current_node in visited:
continue
visited.append(current_node)
children = graph[current_node]
for child in children:
queue.append(child)
print(f'Visiting node {current_node}')
if __name__ == '__main__':
graph = [[1,2,3], [0], [0,4], [0], [2]]
#visit_depth_first(graph, 0)
visit_breath_first(graph, 0)
Run this code and examine the output which should be similar to the following:
# Output from calling visit_breath_first Visiting node 0 Visiting node 1 Visiting node 2 Visiting node 3 Visiting node 4
Notice that in the first run as soon as node 2 was visited, node 4 followed. But in the breath first ordering, When node 2 was visited, node 3 came next. The algorithm only moved to the children of node 2 after all of node 2’s siblings were visited (nodes 1 and 3). The amazing thing is that all we had to do was change the stack to a queue. In Python, we can use the list as a stack or queue. The append method always adds the new element to the end of the list. A pop will remove the last element added. However, you can also pass an index value to pop to tell it to remove the item at a certain index. In the breath first code, we take advantage of this and pass the index 0 to the pop method. This means we are always adding new nodes to the end of the list but taking nodes off the beginning of the list. Thus turning the list into a queue.
Now, play around with passing different starting nodes. Define some graphs of your own and run the program. Check the output and make sure your results are as expected.