Learning Lua Step-By-Step: Part 12

This entry is part 12 of 25 in the series Learning Lua Step-By-Step

Table of Contents

Post Stastics

This post has 1804 words.
Estimated read time is 8.59 minute(s).

Exploring Trees and Graphs in Lua

In this installment of the Learning Lua Step-By-Step series, we delve into the fascinating world of trees and graphs using Lua. Trees and graphs are fundamental data structures in computer science and are widely used for representing relationships and hierarchies. Understanding these structures is crucial for anyone working with data and algorithms. We’ll explore how to create, manage, and leverage trees and graphs in Lua programming.

Understanding Trees and Graphs

Trees

A tree is a hierarchical data structure that consists of nodes connected by edges. It has a root node at the top, with child nodes branching out from it. Each node can have zero or more child nodes, forming a tree-like structure. Trees are used to represent hierarchical relationships, such as family trees, organizational charts, and file system structures.

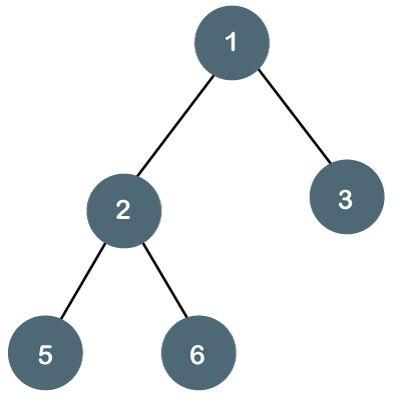
Trees never have cycles. If a tree contains a cycle then it is more properly referred to as a graph.

Graphs

A graph is a collection of nodes (vertices) connected by edges (links). Unlike trees, graphs can have cycles and can be directed or undirected. They are used to model various real-world scenarios, such as social networks, transportation networks, and dependency relationships in software.

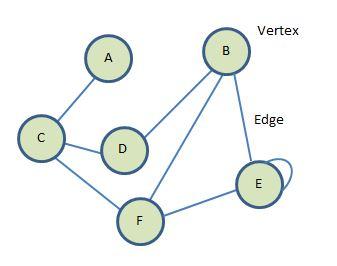
In the above graph, there is a cycle (loop) from C->D->B->F->C. And another cycle from C->D->B->E->F->C, and yet another from E->E. A is the only node that does not participate in a cycle.

Graphs can be classified as either directed or undirected, depending on the nature of the connections between the nodes. In an undirected graph, the edges between nodes are bidirectional, meaning that the connection between two nodes goes both ways. For example, if there is an edge between node A and node B, it indicates that there is a relationship or connection between the two nodes, but the relationship is not necessarily one-way. In contrast, a directed graph, also known as a digraph, has edges that have a specific direction, where the connection between two nodes only goes one way. In a directed graph, the edge between node A and node B would indicate that there is a relationship from A to B, but not necessarily from B to A. This distinction is important when modeling real-world scenarios, as directed graphs can better represent relationships with a clear direction, such as in transportation networks, social networks, or computer networks.

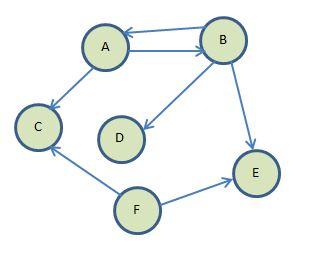
In the graph above, there is a cycle between A->B->A. Note that the connecting lines (Edges/Verticies) have arrows to show their direction of travel. Between A and B you can travel in either direction. Between A and C, you can only travel from A to C.

Graphs can also be classified as weighted or unweighted, depending on whether the edges have associated numeric values or not. In an unweighted graph, the edges between nodes are treated equally, with no additional information about the strength or cost of the connection. However, in a weighted graph, each edge is assigned a numerical weight or cost, which can represent various properties, such as distance, time, or monetary value. This additional information can be crucial in many real-world applications, as it allows for more accurate modeling and optimization of processes.

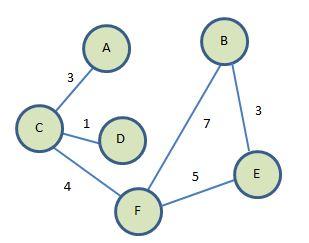
Weighted graphs place cost values on the edges (vertices). A weighted edge is like a tool road. You may drive down it but it will cost you. Typically, the greater the weight, the greater the cost.

For example, in a transportation network, the weights on the edges could represent the distance or travel time between two locations, allowing for the efficient calculation of the shortest or fastest route between destinations. Similarly, in a social network, the weights on the edges could represent the strength of the relationships between individuals, enabling the identification of influential or closely-connected nodes. Weighted graphs provide more nuanced and realistic representations of complex systems, making them a powerful tool in various domains, including logistics, communication, and decision-making.

Implementing Trees and Graphs in Lua

Trees in Lua

Let’s start by creating a basic binary tree in Lua. We’ll define a Node class to represent each node in the tree and a BinaryTree class to manage the tree structure.

-- Node class to represent a node in the binary tree
Node = {}
Node.__index = Node

function Node:new(value)
    local node = {}
    setmetatable(node, Node)
    node.value = value
    node.left = nil
    node.right = nil
    return node
end

-- BinaryTree class to manage the binary tree structure
BinaryTree = {}
BinaryTree.__index = BinaryTree

function BinaryTree:new()
    local tree = {}
    setmetatable(tree, BinaryTree)
    tree.root = nil
    return tree
end

function BinaryTree:insert(value)
    local new_node = Node:new(value)
    if self.root == nil then
        self.root = new_node
    else
        self:_insert_recursive(self.root, new_node)
    end
end

function BinaryTree:_insert_recursive(current, new_node)
    if new_node.value < current.value then
        if current.left == nil then
            current.left = new_node
        else
            self:_insert_recursive(current.left, new_node)
        end
    else
        if current.right == nil then
            current.right = new_node
        else
            self:_insert_recursive(current.right, new_node)
        end
    end
end

-- Example usage
local tree = BinaryTree:new()
tree:insert(5)
tree:insert(3)
tree:insert(8)

This code defines a simple binary tree with insertion functionality. Let’s further expand it with traversal methods like inorder, preorder, and postorder traversal.

Traversal Methods for Trees and Graphs

Tree Traversal Methods

Inorder Traversal: In inorder traversal, we visit the left subtree, then the root node, and finally the right subtree. This traversal method is commonly used for binary search trees to visit nodes in sorted order.

   function BinaryTree:inorder_traversal(node)
       if node == nil then
           return
       end
       self:inorder_traversal(node.left)
       print(node.value)
       self:inorder_traversal(node.right)
   end

   -- Example usage
   tree:inorder_traversal(tree.root)

Preorder Traversal: In preorder traversal, we visit the root node first, then the left subtree, and finally the right subtree. This traversal method is useful for creating a copy of the tree or prefix notation in mathematical expressions.

   function BinaryTree:preorder_traversal(node)
       if node == nil then
           return
       end
       print(node.value)
       self:preorder_traversal(node.left)
       self:preorder_traversal(node.right)
   end

   -- Example usage
   tree:preorder_traversal(tree.root)

Postorder Traversal: In postorder traversal, we visit the left subtree, then the right subtree, and finally the root node. This traversal method is commonly used for deleting nodes from a binary search tree.

   function BinaryTree:postorder_traversal(node)
       if node == nil then
           return
       end
       self:postorder_traversal(node.left)
       self:postorder_traversal(node.right)
       print(node.value)
   end

   -- Example usage
   tree:postorder_traversal(tree.root)

Graph Traversal Methods

Depth-First Search (DFS): DFS explores as far as possible along each branch before backtracking. It’s used to search for a path between two nodes or to traverse the entire graph.

   function Graph:dfs(start)
       local visited = {}
       local stack = {start}
       while #stack > 0 do
           local node = table.remove(stack)
           if not visited[node] then
               visited[node] = true
               print(node)
               for _, neighbor in ipairs(self.vertices[node]) do
                   if not visited[neighbor] then
                       table.insert(stack, neighbor)
                   end
               end
           end
       end
   end

   -- Example usage
   graph:dfs('A')

Breadth-First Search (BFS): BFS explores all neighbors of a node before moving to the next level. It’s useful for finding the shortest path in unweighted graphs or for exploring the entire graph level by level.

   function Graph:bfs(start)
       local visited = {}
       local queue = {start}
       while #queue > 0 do
           local node = table.remove(queue, 1)
           if not visited[node] then
               visited[node] = true
               print(node)
               for _, neighbor in ipairs(self.vertices[node]) do
                   if not visited[neighbor] then
                       table.insert(queue, neighbor)
                   end
               end
           end
       end
   end

   -- Example usage
   graph:bfs('A')

Trees and graphs are important data structures in computer science. There are many traversal algorithms to help you find information about your graph data. Companies like Facebook, Google, ect. keep their algorithms secret for things like who are you connected to and how strong is that connection, is it a family connection? (Facebook), or are these two pages closely related? Do they discuss the same topic, etc. (Google). Graphs can help you learn a lot about your data and can provide efficient look-up algorithms. It is important to know the basics of trees and graphs as they can turn a lengthy calculation into a fast and simple one. Some CS (Computer Science) problems can’t be solved without them. At least not in a reasonable amount of time.

Discussion of Traversal Methods

Inorder Traversal: Useful for visiting nodes in sorted order in binary search trees, helpful for binary search and finding the closest value in a BST.
Preorder Traversal: Useful for creating a copy of the tree or evaluating prefix notation expressions in arithmetic.
Postorder Traversal: Useful for deleting nodes from a binary search tree or evaluating postfix notation expressions in arithmetic.
Depth-First Search (DFS): Suitable for exploring all possible paths in a graph and finding a path between two nodes. It’s often used in maze-solving algorithms and topological sorting.
Breadth-First Search (BFS): Suitable for finding the shortest path in unweighted graphs or exploring a graph level by level. It’s used in network routing algorithms and analyzing social networks.

Understanding these traversal methods is crucial for effectively working with trees and graphs in Lua programming.

Graphs in Lua

Next, let’s create a directed graph in Lua using an adjacency list representation. We’ll define a Graph class to manage the graph structure.

-- Graph class to represent a directed graph using adjacency list
Graph = {}
Graph.__index = Graph

function Graph:new()
    local graph = {}
    setmetatable(graph, Graph)
    graph.vertices = {}
    return graph
end

function Graph:add_vertex(vertex)
    self.vertices[vertex] = {}
end

function Graph:add_edge(from, to)
    table.insert(self.vertices[from], to)
end

-- Example usage
local graph = Graph:new()
graph:add_vertex('A')
graph:add_vertex('B')
graph:add_vertex('C')
graph:add_edge('A', 'B')
graph:add_edge('A', 'C')

This code defines a directed graph with vertices ‘A’, ‘B’, and ‘C’, and edges from ‘A’ to ‘B’ and ‘A’ to ‘C’. You can further enhance it with traversal algorithms like depth-first search (DFS) and breadth-first search (BFS).

Exercise

Implement a function to perform inorder traversal on the binary tree.
Implement depth-first search (DFS) traversal on the graph.
Use a binary tree to sort letters of the alphabet.

Conclusion

Trees and graphs are versatile data structures that play a vital role in various computational tasks. In Lua, you can implement these structures efficiently using object-oriented programming techniques and Lua’s flexible syntax. Understanding how to create, manage, and traverse trees and graphs will greatly enhance your problem-solving skills in programming.

Resources

Lua Documentation: https://www.lua.org/docs.html
Data Structures and Algorithms in Lua: https://www.amazon.com/Data-Structures-Algorithms-Lua-Roberto/dp/1466565279

Series Navigation<< Learning Lua Step-By-Step (Part 10)Learning Lua Step-By-Step (Part 13) >>